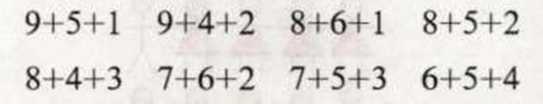问题:将编号从1到9的棋子按一定的方式填入右图中的9个小格中,使得每一行、列以及两条对角线上的和都分别相等。

答案:图中的9个数字相加之和为45。因为方块中的3行(或列)都分别包括数字1到9当中的1个,将这 9个数字相加之和除以3便得到“魔 数”——15。总的来说,任何n阶魔方的“魔数”都可以很容易用这个公式求出:和为15的三数组合有8种可能性:方块中心的数字必须出现在这些可能组合中的4组。5是唯一在4组三数组合中都出现的。因此它必然是中心数字。9只出现于两个三数组合中。因此它必须处在边上的中心,这样我们就得到完整的一行:9+5+1。3和7也是只出现在2个三数组合中。剩余的4个数字只能有一种填法。