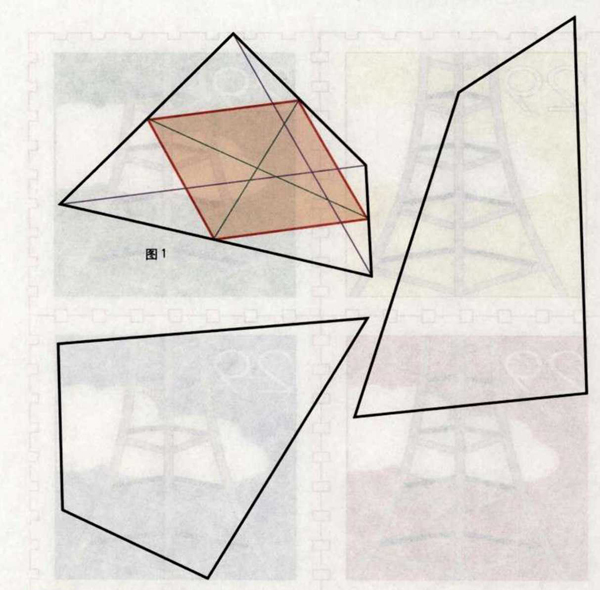
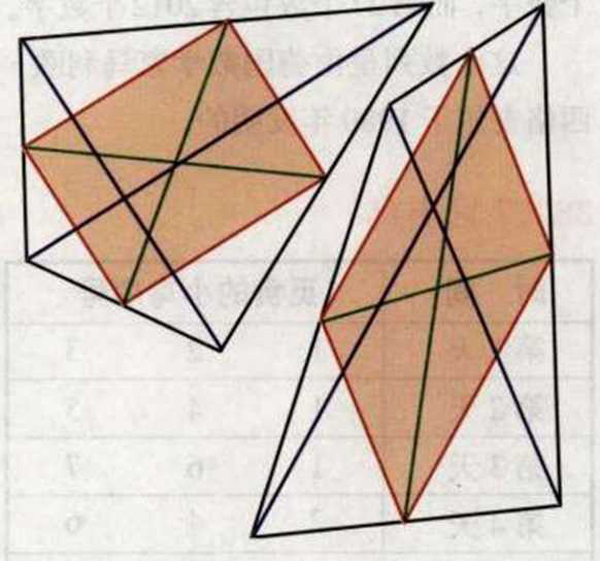问题:右图是3个任意四边形。把图1中的四边形的4条边的中点连接起来,就形成一个平行四边形。且这个平行四边形的边分别与原四边形的2条对角线平行。问这个平行四边形与原四边形的面积之间存在什么关系?平行四边形的周长与原四边形的对角线长度又有什么关系?其他的任意四边形4条边的中点相连也会得到一个平行四边形吗?你可以在所给的另外2个任意四边形上试试。
答案:我们可以发现,所有任意四边形四边中点的连线都会组成一个平行四边 形,我们将这个平行四边形称之为伐里农平行四边形,是以数学家皮埃尔•伐里农(1654〜1722)的名字命名的。伐里农平行四边形的面积是原四边形的面积的一半,而它的周长则等于原四边形2条对角线的长度之和。